Benchmarks
This page shows how FLINT compares to other software on a selection of artificial benchmarks.
Polynomial factorisation over Z/pZ
Time (s) to factor the degree-n polynomial (x + 2x + 3x3 + ... + nxn) modulo 17. CPU: AMD Opteron 6174 2.20 GHz, except Mathematica which was timed on a Xeon E5-2650, 2.00 GHz (>20% faster). FLINT, NTL and presumably also Magma use similar implementations of the Cantor-Zassenhaus algorithm with the Kaltofen-Shoup improvement, so this benchmark largely tests the speed of polynomial arithmetic.
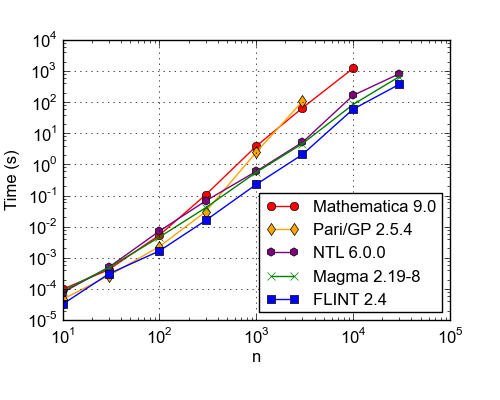
| n | Mathematica 9.0 | Pari/GP 2.5.4 | NTL 6.0.0 | Magma 2.19-8 | FLINT 2.4 |
|---|---|---|---|---|---|
| 10 | 0.000097 | 0.000046 | 0.000076 | 0.000085 | 0.000032 |
| 30 | 0.000415 | 0.000266 | 0.000493 | 0.000480 | 0.000303 |
| 100 | 0.00534 | 0.00229 | 0.00721 | 0.00461 | 0.00166 |
| 300 | 0.105 | 0.0303 | 0.0670 | 0.0404 | 0.0158 |
| 1000 | 3.88 | 2.46 | 0.601 | 0.559 | 0.228 |
| 3000 | 65.8 | 107 | 5.15 | 4.67 | 2.09 |
| 10000 | 1229 | - | 166 | 84.8 | 59.8 |
| 30000 | - | - | 825 | 664 | 376 |
Arithmetic with p-adic numbers
Time (s) to compute a p-adic logarithm to precision 17n. CPU: Xeon X5670, 2.93 GHz. FLINT uses rectangular splitting series evaluation for small n and an asymptotically optimal algorithm (based on balanced argument reduction and binary splitting series evaluation) for large n.
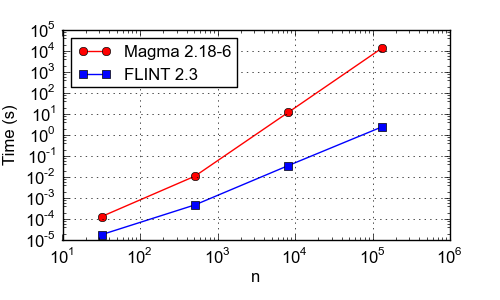
| n | Magma 2.18-6 | FLINT 2.3 |
|---|---|---|
| 32 | 0.000131 | 0.000018 |
| 512 | 0.011 | 0.00047 |
| 8192 | 12 | 0.035 |
| 131072 | 13388 | 2.4 |
Factorisation of word-size integers
Time (s) to factor 10000 consecutive n-bit integers (2n-1 + 1), ..., (2n-1 + 10000), where n goes up to the word size (64 bits). CPU: Xeon E5-2650, 2.00 GHz. FLINT uses a combination of trial division, Hart's One Line Factor algorithm, SQUFOF, and quick tests for primes and perfect powers. The slowdown very close to 64 bits is possibly due to the fact that FLINT does not currently use the p+1 algorithm.
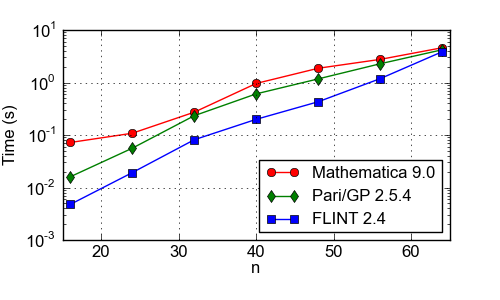
| n | Mathematica 9.0 | Pari/GP 2.5.4 | FLINT 2.4 |
|---|---|---|---|
| 16 | 0.0720 | 0.0160 | 0.00476 |
| 24 | 0.108 | 0.0560 | 0.0192 |
| 32 | 0.272 | 0.233 | 0.0812 |
| 40 | 0.960 | 0.608 | 0.199 |
| 48 | 1.87 | 1.17 | 0.430 |
| 56 | 2.76 | 2.28 | 1.19 |
| 64 | 4.60 | 4.21 | 3.86 |
Power series over the real numbers
Time (s) to compute the Taylor series exp(exp(1+x)) to order xn at n-digit precision. CPU: Xeon E5-2650, 2.00 GHz. For large n, this example illustrates FLINT's efficient arithmetic with polynomials that have both high degree and large coefficients. It should be noted that the timings are not perfectly comparable since the results have different accuracy. Only FLINT 2.4/Arb computes rigorous error bounds.
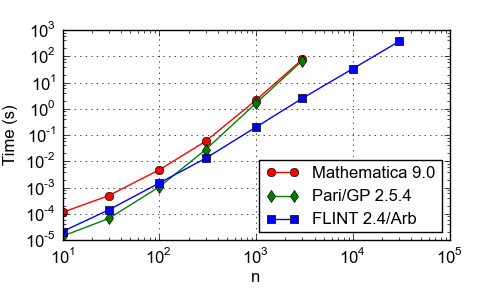
| n | Mathematica 9.0 | Pari/GP 2.5.4 | FLINT 2.4/Arb |
|---|---|---|---|
| 10 | 0.000113 | 0.000014 | 0.000021 |
| 30 | 0.000490 | 0.000066 | 0.000141 |
| 100 | 0.00473 | 0.00106 | 0.00149 |
| 300 | 0.0575 | 0.0276 | 0.0129 |
| 1000 | 2.17 | 1.66 | 0.215 |
| 3000 | 77.0 | 68.7 | 2.51 |
| 10000 | - | - | 34.1 |
| 30000 | - | - | 371 |
Generating Bernoulli numbers
Time (s) to generate a table of the Bernoulli numbers B0, ..., Bn as exact fractions. CPU: Xeon E5-2650, 2.00 GHz. Pari/GP and FLINT 2.4/Arb compute the Bernoulli numbers by numerical approximation of the Riemann zeta function.
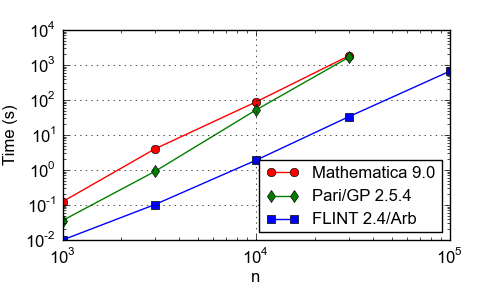
| n | Mathematica 9.0 | Pari/GP 2.5.4 | FLINT 2.4/Arb |
|---|---|---|---|
| 1000 | 0.124 | 0.0360 | 0.0100 |
| 3000 | 4.01 | 0.913 | 0.103 |
| 10000 | 88.8 | 52.4 | 1.92 |
| 30000 | 1817 | 1653 | 33.2 |
| 100000 | - | - | 669 |
Integer partitions
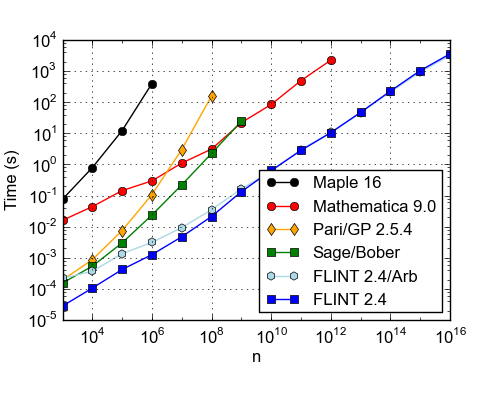
Time (s) to compute the exact value of the partition function p(n). CPU: Xeon X5675, 3.07 GHz. All implementations (except Maple?) use the numerical Hardy-Ramanujan-Rademacher formula. Out of the two FLINT implementations, the newer "FLINT 2.4/Arb" version implements a provably correct algorithm (the older "FLINT 2.4" version depends on heuristics, with most of the speedup for very small n coming from use of hardware floating-point arithmetic).
Last updated: 2022-05-20 09:07:08 GMT
Contact: Fredrik Johansson, flint-devel mailing list.